一、计算题
第一章 图像处理概述
计算图片文件大小最终结果一般要化为字节,或者KB、MB:
BMP格式图片 ★
公式1:
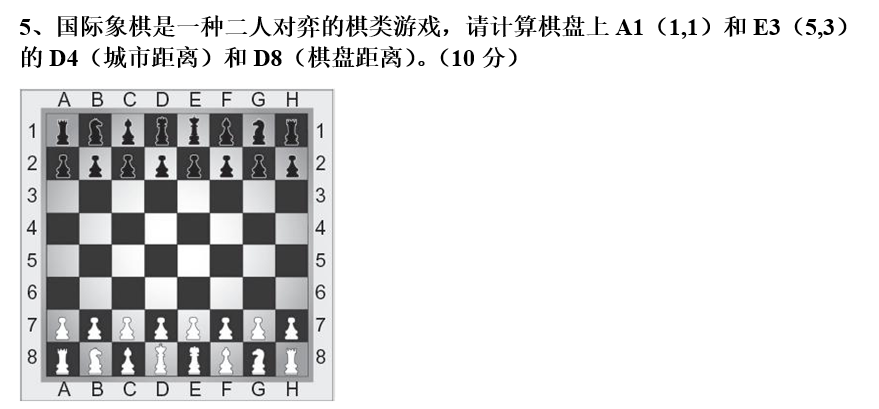
文件头:14B
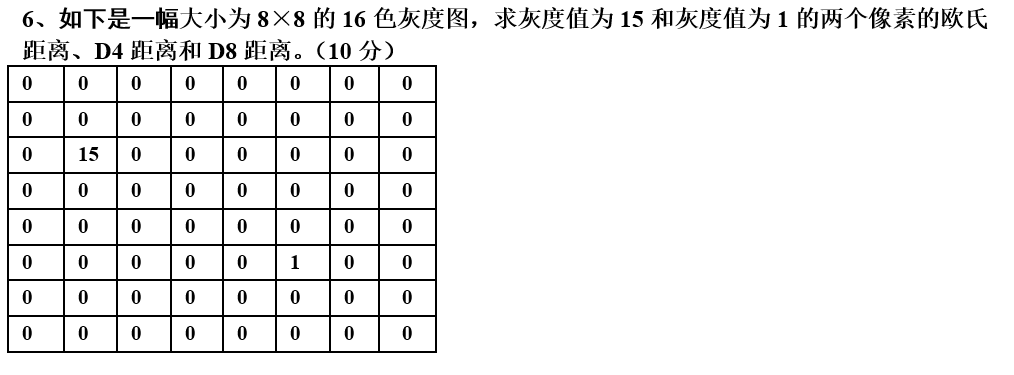
信息头:40B
颜色表:颜色数 × 4(BMP格式通常使用4个字节来保存颜色信息,分别表示红绿蓝和保留字节)
分辨率:行像素数 × 列像素数
位深:256色就是8位深
例题:


公式2:
BMP要求每行的字节数是4的倍数,如果遇到行不是4的倍数需要加上31补齐,使其能够向下取整到最接近的4的倍数:
⚠️注意:上式中的4不能和分母中的32约掉,还有括号不能省去,否则会失去求整的效果。
例题:


PNG格式图片 ★
如果题目未说明,默认为PNG或者无压缩:
例题:

彩色图像没有提 色深度 or 位深 默认为8位深,即RGB三基色,每个基色通常用8bit来表示(256色) → 共24bit,存储每个像素的颜色信息需要3字节
彩色位图
PS:不需要颜色表。
第二章 图像处理基础知识
灰度值的均值、方差和标准差(用灰度值替换x)
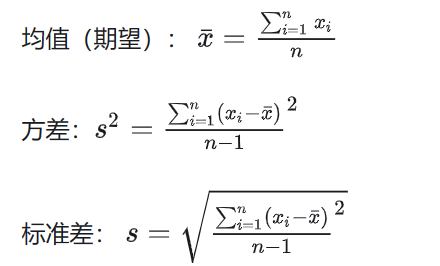
RGB模型 ↔ HSL模型
(教材P30,老师说用不到计算器,感觉考得概率很小?)
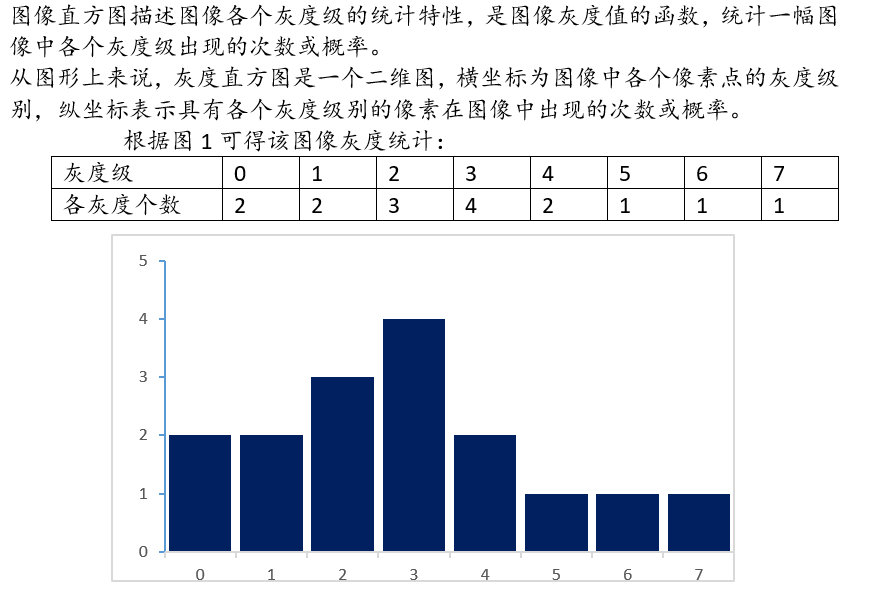
直方图 ★
一般灰度直方图:
横坐标:灰度值
纵坐标:具有该灰度级的像素个数
归一化直方图:
横坐标:灰度值
纵坐标:具有该灰度级的像素出现的频数(像素个数 / 像素总数)
例题:

像素间的关系:
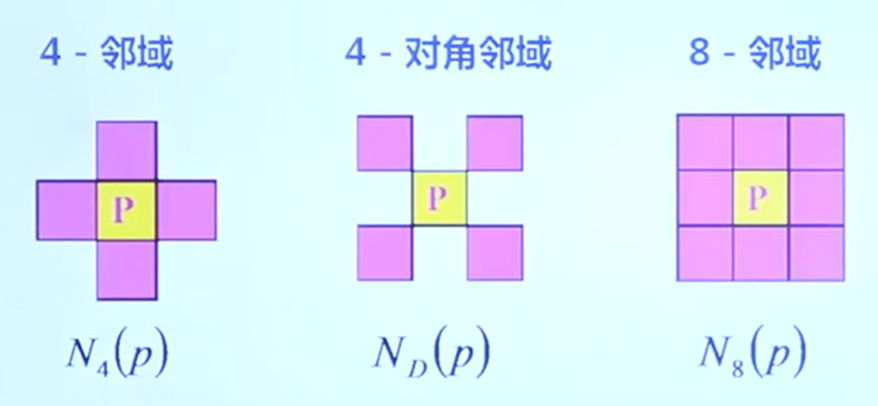
如果两个像素点邻接,需要满足:
- 互为领域
- 灰度值相似
设置一个相似灰度值集合V,例如V = {16, 17, …, 32},如果p,q的灰度值都在V中,且 $q∈N_4(p) $,则p、q为4-邻接。
m-邻接:如果像素点的灰度值满足相似性准则,又满足下列条件之一:
$q∈N_4(p) $
$q∈N_D(p) $ 且 $N_4(p) ∩ N_4(p) = ∅$
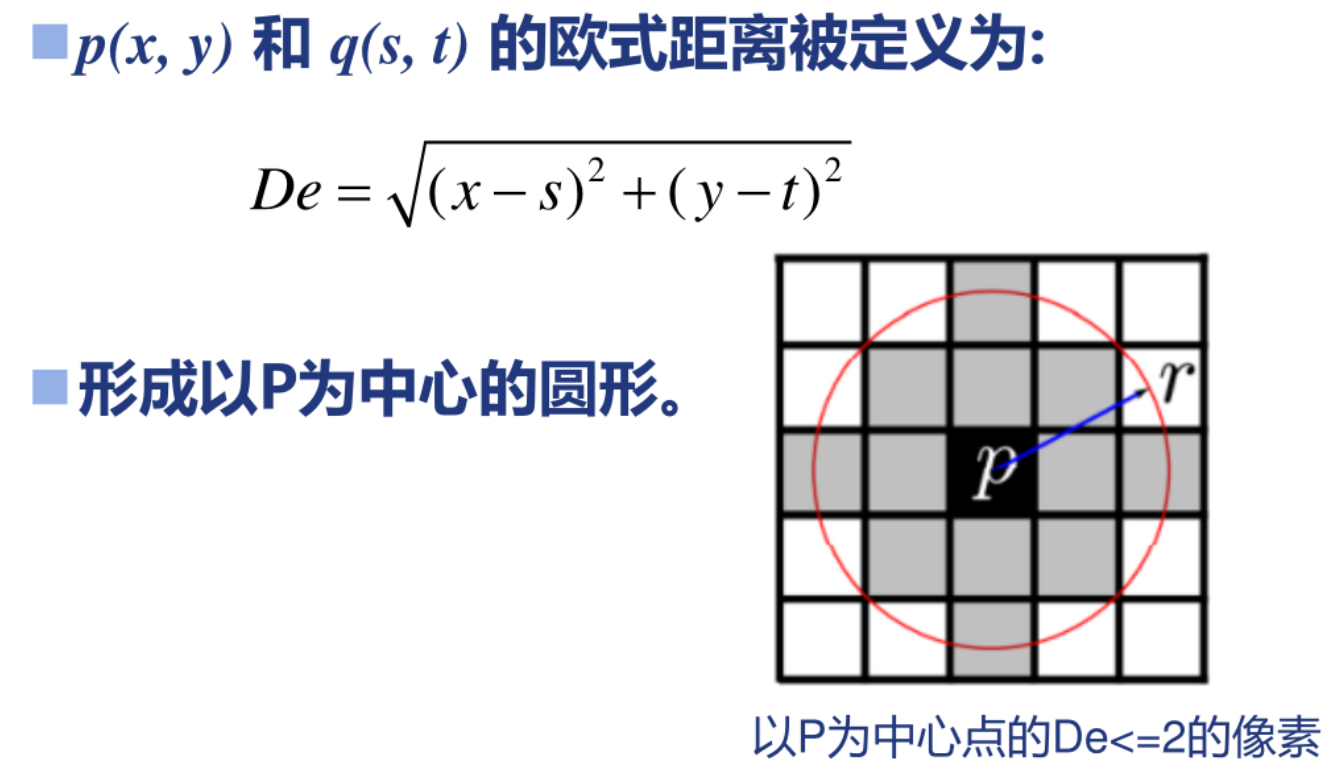
距离通量 ★
1. 欧式距离 $D_e $
2. 城市街道距离 $D_4 $

⚠️ $D_4(p, q) = 1 $ 时,q是p的4领域。
3. 棋盘距离 $D_8 $

⚠️ $D_e $、 $D_4 $、 $D_8 $ 距离仅与像素点的坐标有关,与图像内容没有关系。
4. $D_m $距离:
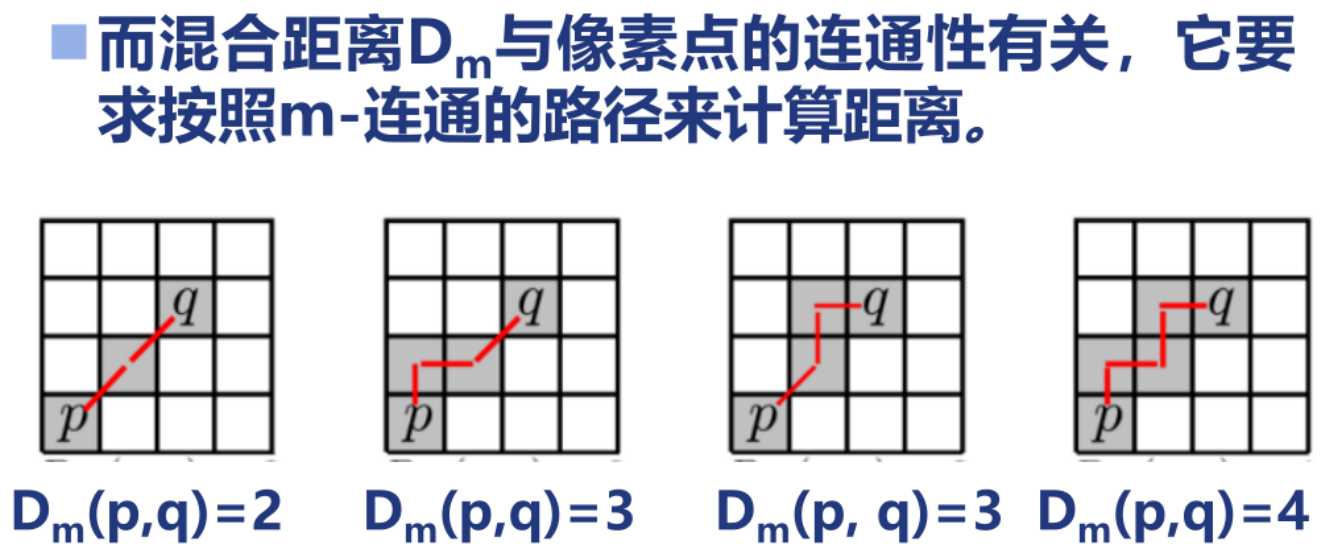
例题1:

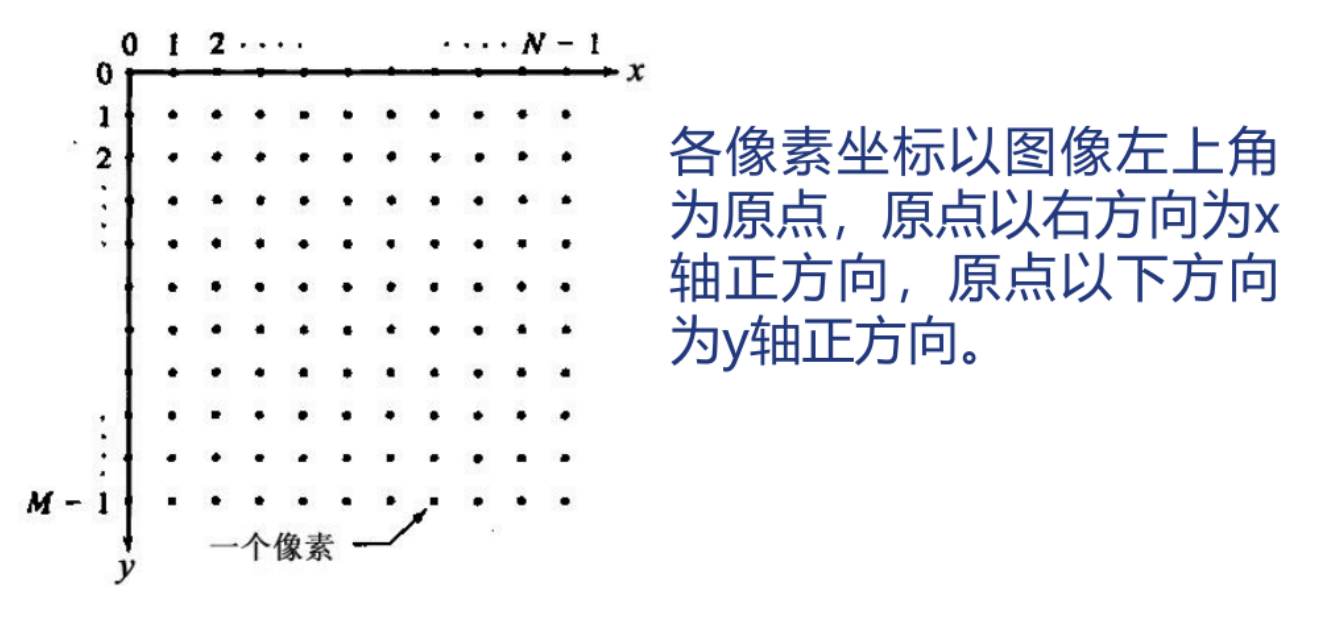
⚠️坐标约定:
例题2:

图像质量评价 ★
(过于复杂的题目应该会给公式?)
1. MSE均方误差
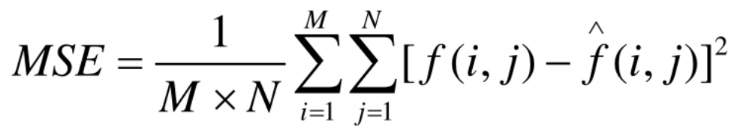
2. SNR信噪比
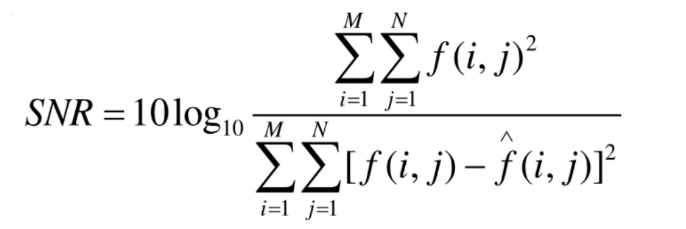
3. PSNR峰值信噪比
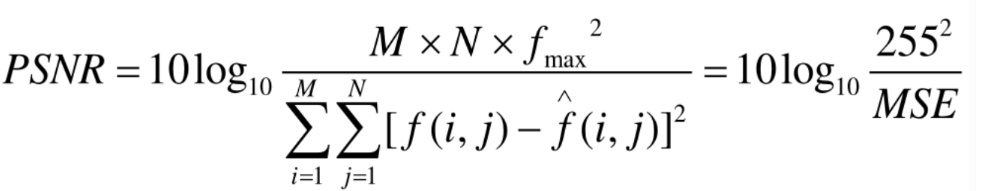
4. MAE平均绝对误差
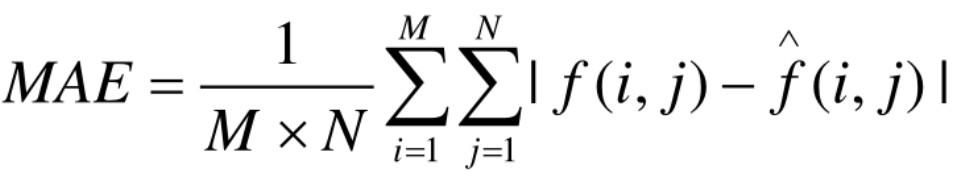
5. SSIM结构相似性
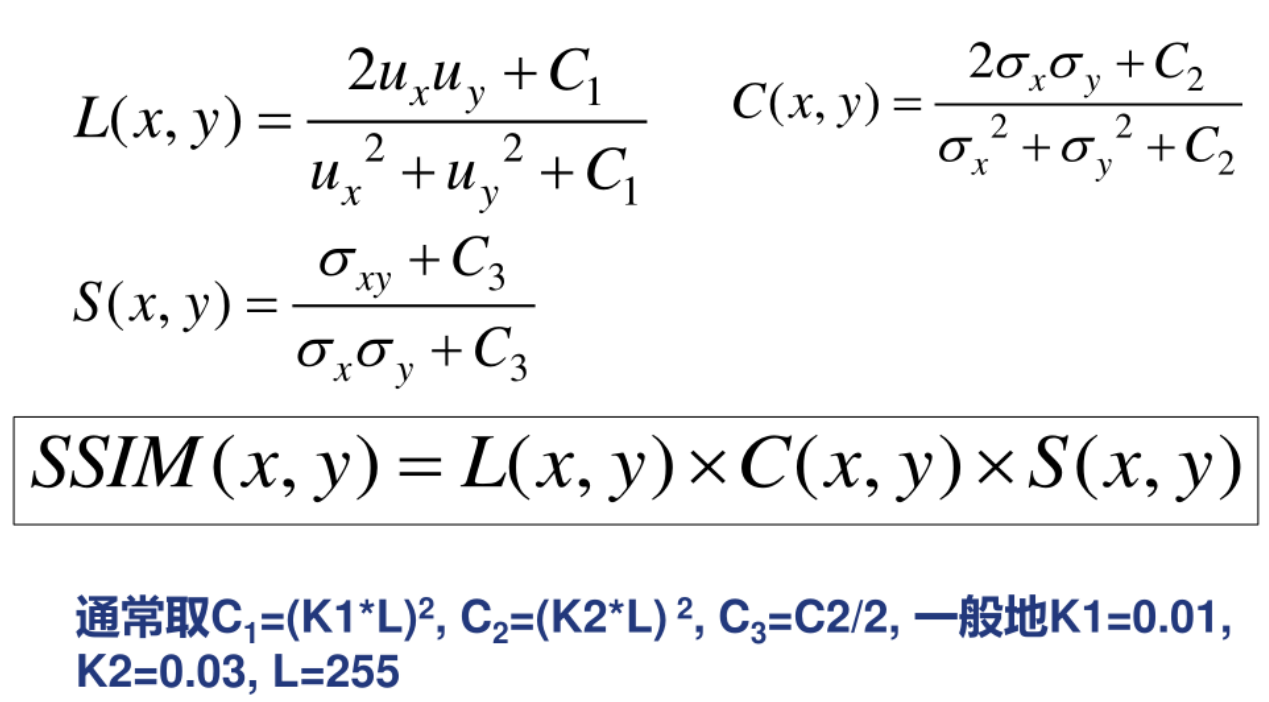
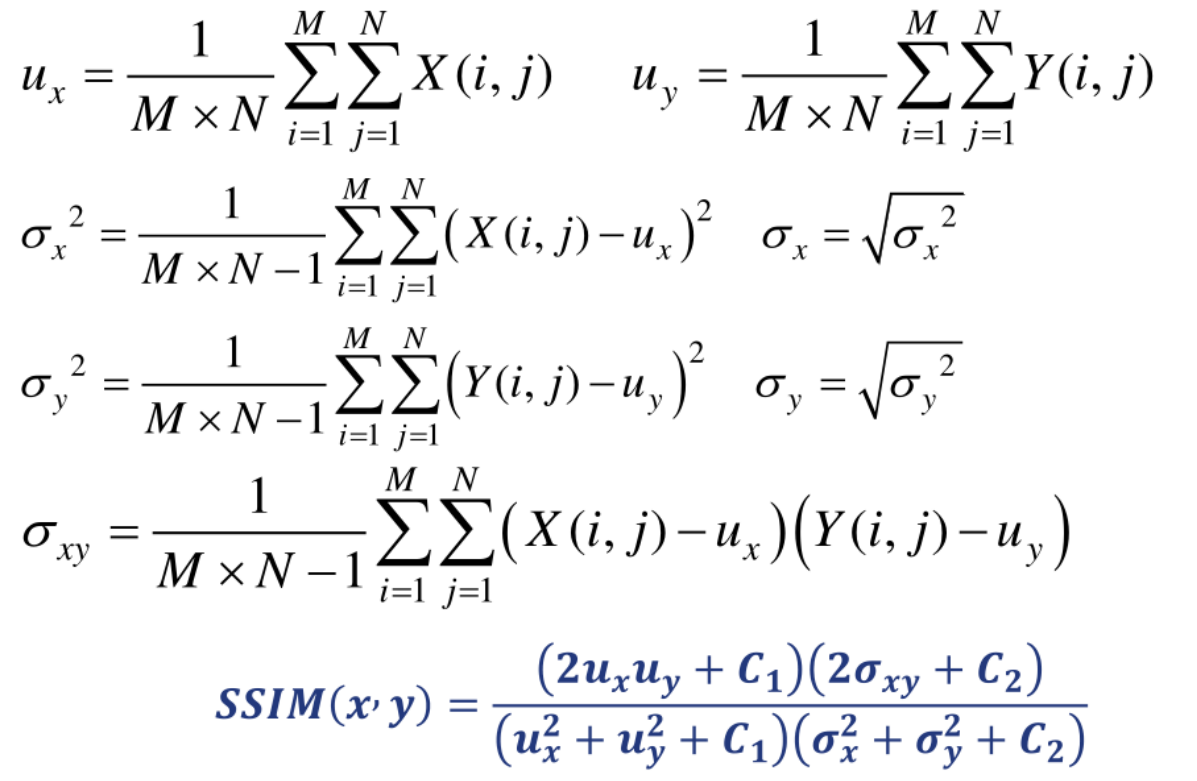
例题:


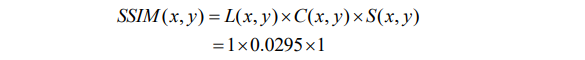
第三章 空域图像增强
线性灰度变换 ★
全局线性变换★
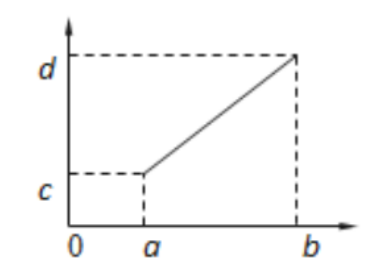
横轴:原图像的输入灰度值,范围为[a, b]
纵轴:变换后图像的输出灰度值,范围为[c, d]
将原图像的灰度值范围[a, b]变换到[c, d],输入图像灰度值 r 与输出图像灰度值 s 之间的关系式为:
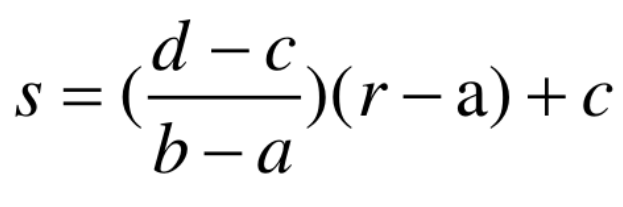
斜率等于1,经过全局变换后,灰度值动态范围不会有变化;
斜率大于1,……扩展;
斜率小于1,……压缩。
分段线性变换
(原理同全局线性变换,课本P48)
图像反转
$s = (L-1) -r $ 或者 $s = 1.0-r $ (归一化灰度值)
$L $为图像的灰度级。
灰度图像阈值化

基于直方图的灰度变换 ★
直方图均衡化(必考)★
灰度变换函数必须满足:
- $T(r) $ 在 $0≤r≤1 $ 区间内是单值函数(对定义域每一个自变量x,其对应的函数值f(x)是唯一的),且单调递增(保证原始灰度级的次序)
- $T(r) $ 在 $0≤r≤1 $ 区间内满足 $0≤T(r)≤1 $ (保证映射后的像素灰度级仍在允许灰度级范围内,避免整个图像明显变亮或变暗)
例题:


量化,即找与 $s_k $ 最接近的量化灰度级 $r_k $ ,比如上表中 $s_k = 0.44 $ 最接近它的灰度级是 $r_k = 0.43 $ ,因此映射为 $1/7→3/7 $
直方图规定化
(课本P58,张老师原话“比较麻烦”,可能不会考)
空域滤波与邻域运算 ★
领域运算(滤波操作)
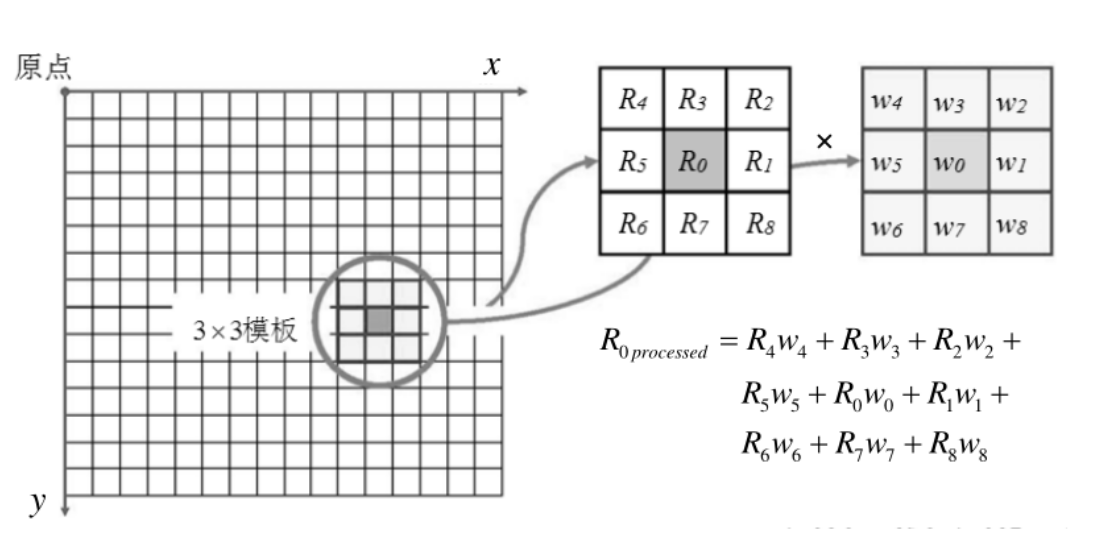
⚠️滤波操作是相关运算。
空域平滑滤波 ★
均值滤波
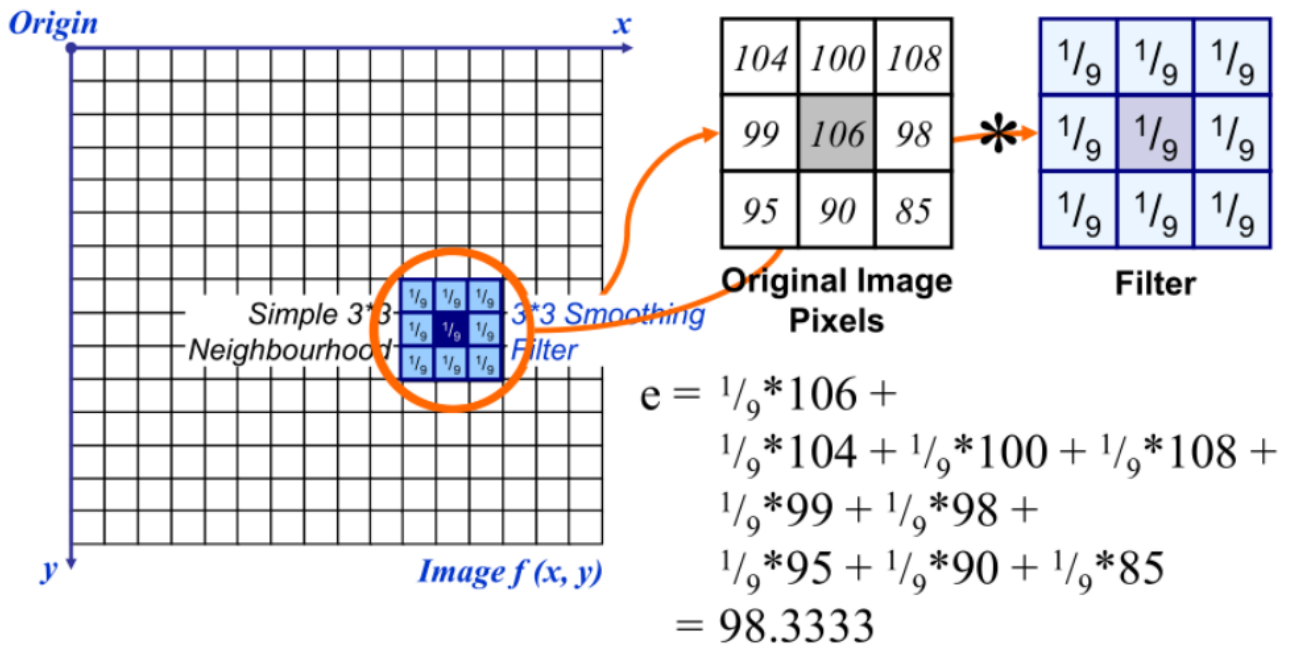
例题:


边界处理★
常量法(通常是补0)方式扩展边界:

反射法(reflect)方式扩展边界(以边界为轴镜像扩展):
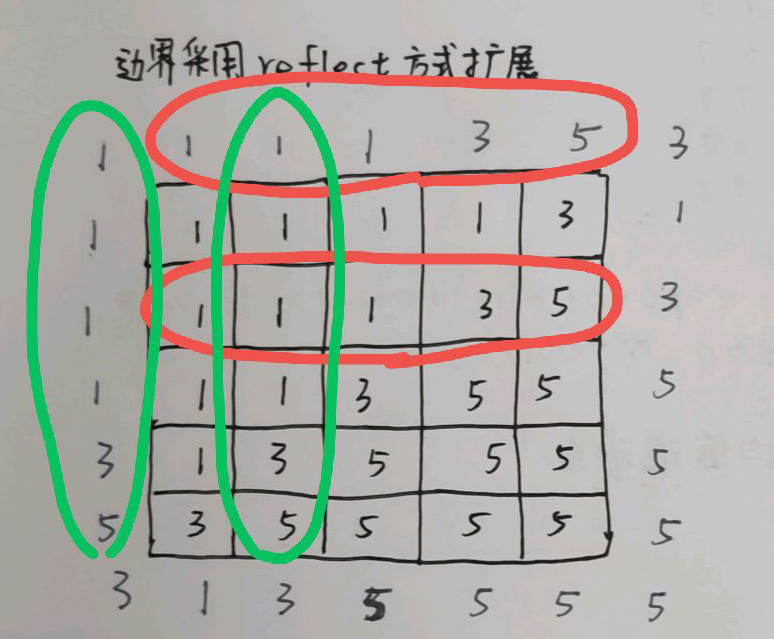
复制法(replicate)方式扩展边界(对边界进行复制):

- 外包装法(wrap):

高斯滤波:(课本P63,应该不会考?)
阈值邻域平滑滤波:
设定一个阈值 $T $,先用均值滤波求出灰度值 $f’(x, y) $,与原来的灰度值 $f(x,y) $相减:

中值滤波:
例题:

空域锐化滤波 ★
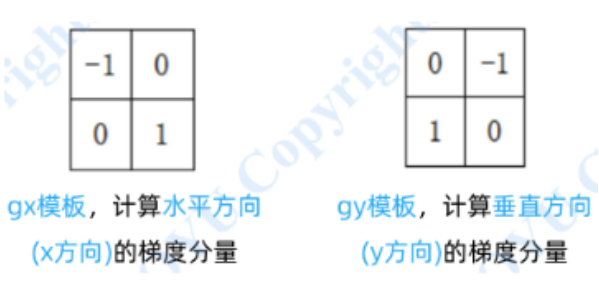
一阶微分算子 ★
Roberts算子:
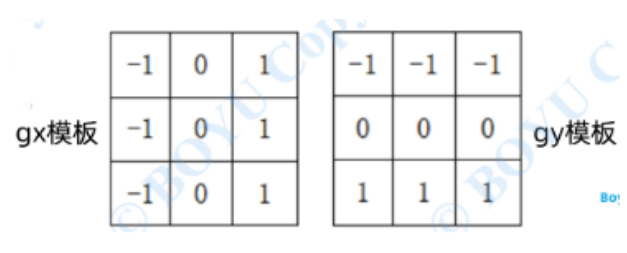
Prewitt算子:
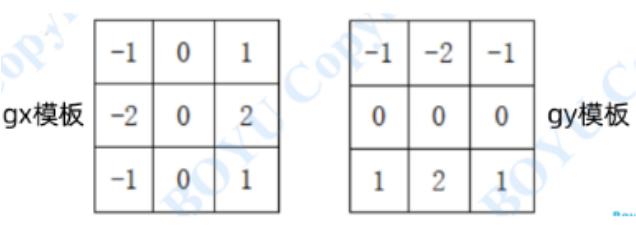
Sobel算子:

例题:


二阶微分算子
(课本P73,主要是拉普拉斯算子,应该不会考?课后习题、学习通作业都没有出过)
相关运算与卷积运算 ★
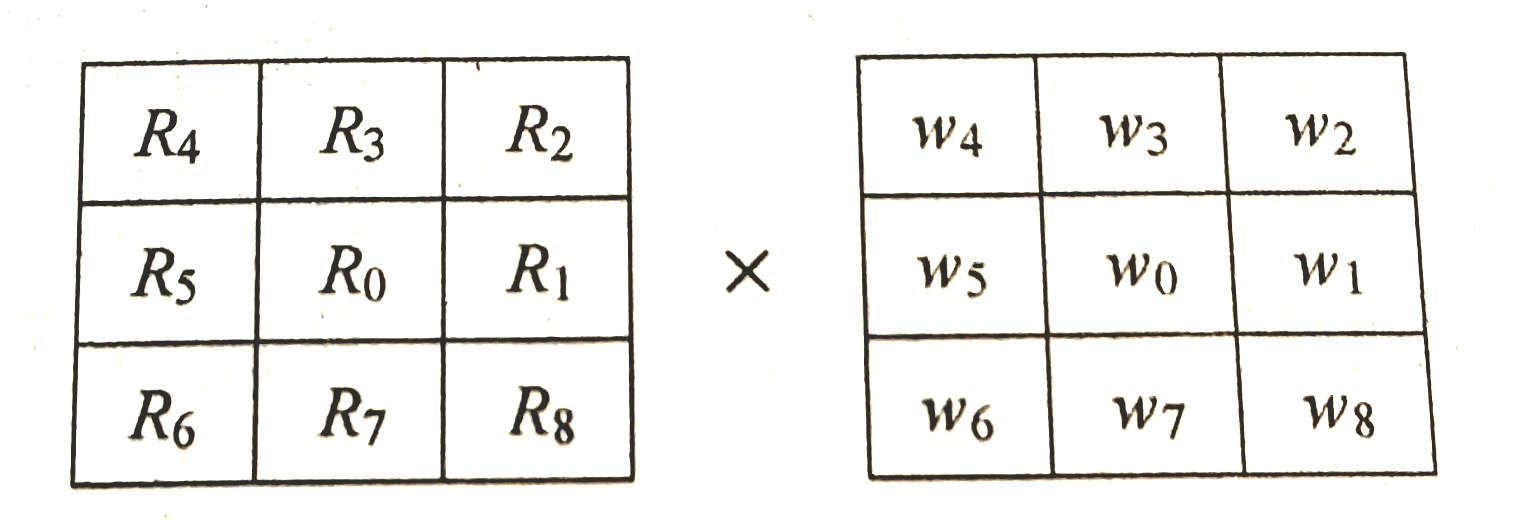
- 相关运算见前“领域运算”
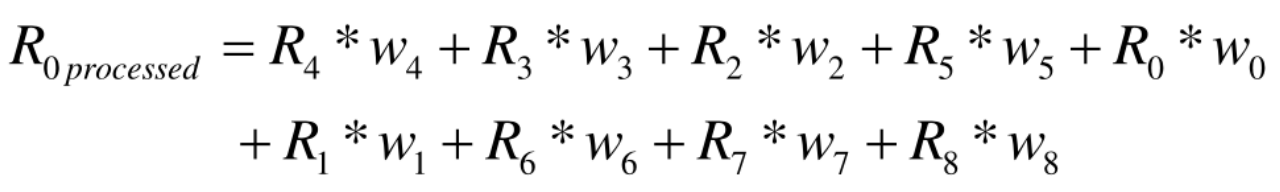
- 卷积运算:先把滤波核进行180°旋转后再进行点乘
第六章 图像的几何变换
改变空间坐标。
